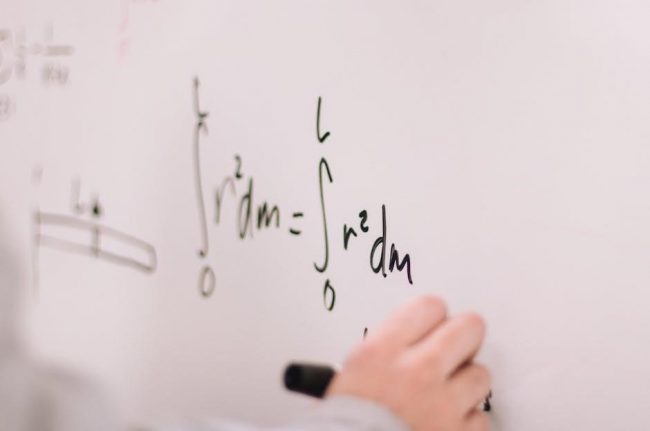Calculus of a single variable, readily available as PDFs, offers a flexible learning experience. Resources like MIT OpenCourseWare and various textbooks provide comprehensive study materials.

Digital formats enhance accessibility, integrating interactive exercises and applets for a dynamic understanding of limits, derivatives, and integrals.
What is Single Variable Calculus?
Single variable calculus fundamentally explores the mathematics of functions with one independent variable. This branch focuses on two core operations: differentiation and integration, building upon the foundation of pre-calculus concepts like limits and continuity;
It’s a crucial stepping stone for students in mathematics, physics, engineering, and economics. PDF versions of classic textbooks, such as Edwards and Penney, and Hughes-Hallett, provide accessible learning materials. The study involves analyzing rates of change (derivatives) and accumulating quantities (integrals), offering powerful tools for modeling real-world phenomena. Interactive resources, like those found on Runestone Academy, complement traditional textbook learning.
Why Use a PDF Textbook?
PDF textbooks for single variable calculus offer unparalleled convenience and cost-effectiveness. They eliminate the need for physical copies, reducing expenses and enabling easy access on various devices. Resources like MIT OpenCourseWare and University of Calicut provide free PDF study materials.
Furthermore, PDFs facilitate searching, highlighting, and note-taking directly within the document. Interactive elements, denoted by “(AP)”, link to applets enhancing understanding. ALEKS integration with PDFs provides personalized learning and reporting. This digital format supports flexible learning schedules and promotes environmentally conscious study habits.

Popular Calculus Textbooks Available as PDFs
Edwards and Penney, Hughes-Hallett, Swokowski, and Houghton Mifflin offer widely-used calculus textbooks frequently found in PDF format for convenient study.
Edwards and Penney, Calculus: Early Transcendentals
Edwards and Penney’s Calculus: Early Transcendentals is a frequently utilized resource, with many students leveraging PDF versions for study. MIT OpenCourseWare’s 18.01SC course notably employs this textbook, and a repository exists containing detailed lecture notes aligned with its chapters.
This textbook is known for its comprehensive coverage of single variable calculus topics, making it a solid foundation for students. The availability of a digital PDF allows for easy access and portability, enhancing the learning process. Interactive exercises, potentially linked via Runestone Academy, complement the traditional textbook material.
Hughes-Hallett, Gleason, et al., Calculus: Single & Multivariable
Hughes-Hallett, Gleason, et al.’s Calculus: Single & Multivariable, in its 6th Edition, is a well-regarded textbook often found as a PDF resource. It continues a tradition of emphasizing conceptual understanding alongside rigorous mathematical development.
The textbook offers a robust approach to single variable calculus, providing students with a strong foundation in the core principles. Digital PDF versions facilitate convenient study, and some editions incorporate interactive applets (marked with “AP”) enhancing engagement. This resource is valuable for both self-study and structured courses, offering a comprehensive learning experience.
Swokowski’s Calculus of a Single Variable
Swokowski’s Calculus of a Single Variable is a classic textbook frequently available in PDF format, offering a time-tested approach to learning calculus. It’s known for its clear explanations and numerous examples, aiding students in grasping fundamental concepts.
Recent changes in calculus education highlight opportunities for improvement in textbooks like Swokowski’s. The PDF version provides accessibility and portability, allowing students to study efficiently. It remains a valuable resource for mastering limits, derivatives, integrals, and their applications, despite evolving pedagogical approaches.
Houghton Mifflin Calculus Textbooks
Houghton Mifflin Calculus textbooks, often found as PDFs, provide comprehensive coverage of single variable calculus. Instructors seeking these resources can contact Houghton Mifflin sales representatives for access. These materials are designed to support a robust learning experience, covering essential topics like limits, differentiation, and integration.
The publisher emphasizes instructor support, offering resources like McDougal to aid in teaching. Modern editions incorporate data-driven insights, including “Capstone” exercises, enhancing student engagement. The PDF format allows for convenient distribution and study, complementing traditional classroom instruction.

Key Topics Covered in Single Variable Calculus PDFs
PDF resources cover core concepts: limits, continuity, derivatives, integrals, and their applications. Interactive elements within textbooks enhance understanding of these fundamental calculus principles.
Limits and Continuity
Limits form the bedrock of calculus, defining how functions behave as inputs approach specific values. PDF textbooks meticulously explain limit calculations, including indeterminate forms and one-sided limits, crucial for understanding function behavior.
Continuity, closely linked to limits, ensures a function’s unbroken nature over an interval. Resources detail different types of discontinuities – removable, jump, and infinite – and their implications. Interactive applets within PDFs often visualize these concepts, aiding comprehension. Mastering limits and continuity is essential before tackling derivatives and integrals, as they establish the foundation for further calculus exploration.
Derivatives
Derivatives, central to single variable calculus, measure a function’s instantaneous rate of change. PDF textbooks like Edwards and Penney thoroughly cover derivative definitions, notations, and computational techniques. They detail basic differentiation rules – power, product, quotient – alongside advanced methods like the chain rule and implicit differentiation.
Many PDF resources now integrate interactive exercises, allowing students to practice applying these rules. Understanding derivatives unlocks applications in optimization, related rates, and curve sketching, demonstrating their power in modeling real-world phenomena. Visual applets within PDFs enhance conceptual understanding.
Basic Differentiation Rules
PDF calculus textbooks systematically present fundamental differentiation rules. The power rule, a cornerstone, simplifies differentiating terms like xn. Product and quotient rules handle functions multiplied or divided, respectively. Constant multiple and sum/difference rules provide further simplification techniques.
Interactive PDFs, particularly those linked to Runestone Academy, often include exercises specifically designed to master these rules. These resources reinforce understanding through practice, building a solid foundation for more complex differentiation techniques. Mastery of these basics is crucial for tackling advanced calculus problems.
Chain Rule
The chain rule, a vital concept in single variable calculus PDFs, addresses differentiating composite functions. It states that the derivative of f(g(x)) is f'(g(x)) multiplied by g'(x). Textbooks like Edwards and Penney dedicate significant space to illustrating this rule with numerous examples.
Interactive PDF resources, marked with (AP), often feature applets demonstrating the chain rule visually. Runestone Academy’s exercises provide targeted practice, solidifying comprehension. Mastering the chain rule is essential for differentiating complex functions encountered in various applications, from related rates to optimization.
Implicit Differentiation
Implicit differentiation, thoroughly covered in single variable calculus PDFs, is crucial when functions aren’t explicitly solved for y. Textbooks, such as Hughes-Hallett’s Calculus, demonstrate differentiating both sides of an equation with respect to x, treating y as a function of x.
This technique is vital for finding derivatives of implicitly defined curves. Interactive resources within PDFs (AP designation) can visually illustrate the process. Runestone Academy offers exercises to practice applying implicit differentiation, building proficiency. Understanding this method expands problem-solving capabilities beyond explicit functions.
Applications of Derivatives
Single variable calculus PDFs extensively explore the applications of derivatives, moving beyond mere computation. Textbooks like Edwards and Penney detail optimization problems – finding maximum or minimum values – and related rates, analyzing changing quantities. The Mean Value Theorem is also a key focus.
These concepts are often presented with real-world examples, enhancing understanding. Interactive elements within PDFs, marked (AP), can visualize these applications. Resources like Runestone Academy provide practice exercises, solidifying skills in applying derivatives to solve practical problems, demonstrating calculus’s power.
Optimization Problems
PDF versions of single variable calculus textbooks, such as those by Hughes-Hallett and Swokowski, dedicate significant sections to optimization problems. These involve finding the maximum or minimum values of a function, often representing real-world scenarios like maximizing area or minimizing cost.
Derivatives are crucial for identifying critical points, where these extrema potentially occur. Interactive resources, indicated by (AP) in PDFs, can visually demonstrate these concepts. Runestone Academy offers exercises to practice applying derivative techniques to solve diverse optimization challenges, building a strong problem-solving skillset.
Related Rates
Single variable calculus PDFs, including Edwards and Penney’s Calculus: Early Transcendentals, thoroughly cover related rates problems. These problems explore how the rates of change of different variables are connected, often involving geometric shapes or physical phenomena.
Successfully tackling these requires implicit differentiation and a clear understanding of the problem’s geometry. Interactive applets (AP designation in PDFs) can help visualize these changing relationships. Resources like MIT OpenCourseWare and Runestone Academy provide practice exercises, solidifying the ability to apply calculus to dynamic situations.
Mean Value Theorem
Calculus of a single variable PDFs, such as those from Hughes-Hallett’s Calculus: Single & Multivariable, dedicate sections to the Mean Value Theorem. This fundamental theorem connects the average rate of change of a function over an interval to its instantaneous rate of change at some point within that interval.
Understanding this theorem is crucial for analyzing function behavior and proving other important results. Interactive resources within PDFs, marked (AP), can visually demonstrate the theorem’s implications. Study materials from the University of Calicut and MIT OpenCourseWare offer detailed explanations and practice problems.
Integrals
PDF versions of single variable calculus textbooks, like Edwards and Penney’s Calculus: Early Transcendentals, thoroughly cover integrals. These resources explore both indefinite and definite integrals, building from the concept of antiderivatives to calculating areas under curves.
A core component is the Fundamental Theorem of Calculus, linking differentiation and integration. Interactive exercises, available through Runestone Academy and potentially embedded within PDFs (AP designation), reinforce understanding. University of Calicut study materials and MIT OpenCourseWare (18.01SC) provide supplementary explanations and practice problems for mastering integral calculus.
Indefinite Integrals
PDF calculus textbooks detail indefinite integrals as the family of functions whose derivative is a given function. Resources like Hughes-Hallett’s Calculus: Single & Multivariable and Swokowski’s Calculus of a Single Variable provide extensive examples and practice.
Understanding the constant of integration, ‘C’, is crucial, as it represents the ambiguity in finding antiderivatives. Interactive exercises within PDFs, marked with (AP), and platforms like Runestone Academy offer practice. MIT OpenCourseWare (18.01SC) supplements textbook learning, solidifying the concept of indefinite integration.
Definite Integrals
PDF calculus resources, including Edwards and Penney’s Calculus: Early Transcendentals, explain definite integrals as representing the net signed area under a curve between two limits. These materials emphasize the Fundamental Theorem of Calculus, linking integration and differentiation.
University of Calicut study materials and interactive PDFs with (AP) designations offer applets to visualize this concept. ALEKS integration with textbook PDFs provides practice and reporting. Mastering definite integrals is key, and resources like MIT OpenCourseWare (18.01SC) aid comprehension.
Fundamental Theorem of Calculus
PDF calculus textbooks, such as Hughes-Hallett’s Calculus: Single & Multivariable, deeply explore the Fundamental Theorem of Calculus, showcasing its two crucial parts. These resources demonstrate how differentiation and integration are inverse processes, linking rate of change to accumulated change.
MIT OpenCourseWare (18.01SC) and interactive PDFs (marked AP) provide visualizations and exercises. ALEKS integration with textbook PDFs offers practice. Understanding this theorem, as presented in Swokowski’s Calculus, is vital for solving problems involving areas and accumulation.
Techniques of Integration
PDF versions of textbooks like Edwards and Penney’s Calculus: Early Transcendentals systematically cover essential integration techniques. The Substitution Rule and Integration by Parts are explained with numerous examples, aiding comprehension. Resources from the University of Calicut provide detailed study materials on these methods.
Runestone Academy’s interactive exercises, often linked to PDFs via (AP) designations, reinforce these concepts. Houghton Mifflin textbooks also present these techniques, preparing students for complex problems. Mastering these skills is crucial for applying calculus effectively.
Substitution Rule
The Substitution Rule, a fundamental integration technique, is thoroughly explained in PDF versions of popular calculus textbooks. Resources like Edwards and Penney’s work and materials from the University of Calicut demonstrate its application with detailed examples. This method simplifies integrals by reversing the chain rule.

Runestone Academy’s interactive exercises, accessible through (AP) marked PDFs, provide practice. Understanding the correct substitution – ‘u’ and ‘du’ – is key. Mastering this rule is essential for solving a wide range of integration problems found in single variable calculus.
Integration by Parts
Integration by Parts, a crucial technique in single variable calculus, is well-documented in PDF versions of standard textbooks. Resources like Hughes-Hallett’s Calculus: Single & Multivariable and Swokowski’s Calculus of a Single Variable offer clear explanations and examples. The formula ∫u dv = uv ⎻ ∫v du is central to this method.
Interactive exercises on platforms like Runestone Academy, linked via (AP) designations in PDFs, help solidify understanding. Choosing appropriate ‘u’ and ‘dv’ is vital. Mastering this technique expands problem-solving capabilities, particularly with products of functions.
Applications of Integrals
PDF versions of calculus textbooks, such as Edwards and Penney’s Calculus: Early Transcendentals, thoroughly cover the Applications of Integrals. Key concepts include calculating the Area Between Curves, utilizing definite integrals to find the precise area enclosed by different functions.
Furthermore, these resources detail Volumes of Solids of Revolution, employing techniques like disk, washer, and shell methods. Interactive applets, accessible through (AP) markings in PDFs, visually demonstrate these applications. Understanding these concepts is crucial for solving real-world problems in engineering and physics.
Area Between Curves

Calculus textbooks in PDF format, like Hughes-Hallett’s Calculus: Single & Multivariable, dedicate sections to finding the Area Between Curves. This involves utilizing definite integrals to determine the area enclosed by two or more functions. The process requires identifying intersection points and setting up the appropriate integral expression.
Interactive resources, often linked within PDFs via (AP) designations, provide visual aids and step-by-step solutions. These PDFs demonstrate how to subtract functions to correctly represent the area, ensuring accurate calculations. Mastering this application is fundamental to understanding integral calculus.

Volumes of Solids of Revolution
Calculus PDF textbooks, such as Edwards and Penney’s Calculus: Early Transcendentals, extensively cover Volumes of Solids of Revolution. This technique employs definite integrals to calculate the volume generated when a region is rotated around an axis.
Methods like the disk, washer, and shell methods are detailed, with examples illustrating their application. Interactive elements within PDFs (marked AP) often visualize these rotations. Understanding these concepts is crucial for solving complex volume problems. Resources from MIT OpenCourseWare complement these textbooks, offering further practice and clarification.

Interactive Resources and PDF Integration
PDFs now integrate interactive elements, like Runestone Academy exercises, and applets (designated AP) enhancing learning. These resources provide dynamic practice alongside traditional calculus textbooks.
Runestone Academy Interactive Exercises
Runestone Academy is developing a substantial collection of interactive exercises specifically designed for calculus students. This initiative aims to provide instructors with a readily available resource to supplement existing textbooks, such as Edwards and Penney’s Calculus: Early Transcendentals.
The platform’s structure allows for seamless integration with various calculus courses, offering a wealth of practice problems. These exercises are designed to reinforce key concepts and build a strong foundation in single variable calculus. The goal is to create a dynamic learning environment, moving beyond static PDF materials.
Instructors can assign these exercises without requiring site licenses or setup fees, making it a cost-effective solution for enhancing student engagement and comprehension.
Applets and Interactive Elements within PDFs (AP designation)
Certain PDF versions of calculus textbooks, notably those from Hughes-Hallett, Gleason, and others, are enhanced with interactive applets. These are clearly marked with an “(AP)” designation within the document. Clicking on this marker directly within the PDF launches a related, dynamic applet or interactive element.
This feature transforms static PDF pages into a more engaging learning experience, allowing students to visualize concepts and manipulate variables. It’s a significant step towards bridging the gap between traditional textbook learning and modern, interactive educational tools.
These applets support understanding of complex topics within single variable calculus, offering a practical complement to theoretical explanations.

Finding and Accessing Calculus of a Single Variable PDFs
PDFs are accessible through MIT OpenCourseWare (18.01SC), University of Calicut study materials, and integrated platforms like ALEKS, offering diverse learning options.
MIT OpenCourseWare (18.01SC)
MIT OpenCourseWare’s 18.01SC course provides a complete single variable calculus experience, freely available online. This resource includes lecture videos, assignments, and importantly, a comprehensive set of notes compiled by a student utilizing Edwards and Penney’s Calculus: Early Transcendentals.
These meticulously crafted notes serve as an excellent companion to the course materials, offering a detailed walkthrough of key concepts. The course’s open nature allows learners to access high-quality educational content without cost, fostering independent study and a deeper understanding of calculus principles. It’s a fantastic starting point for anyone seeking a robust PDF-based learning path.
University of Calicut Study Materials
The University of Calicut’s School of Distance Education offers comprehensive study materials for its second semester B.Sc. Mathematics course, including a dedicated module on Calculus of a Single Variable. These materials are available as PDF documents, providing students with a structured approach to learning fundamental calculus concepts.
The curriculum covers essential topics, designed to build a strong foundation in mathematical analysis. Access to these resources allows students to study at their own pace, reinforcing classroom learning with detailed explanations and practice problems. It’s a valuable resource for self-study and exam preparation.
ALEKS Integration with Textbook PDFs
ALEKS offers a powerful integration with calculus of a single variable textbook PDF pages, enhancing the learning experience without requiring setup or site license fees. For instructors, ALEKS streamlines course management by providing comprehensive reporting on student progress and understanding.
This integration delivers value by offering detailed insights into student performance, allowing educators to tailor instruction effectively. ALEKS can save instructors valuable time while simultaneously providing students with personalized learning paths and targeted practice, ultimately improving comprehension and success in calculus.